200以上 円 角度 求め方 667839-円 角度 求め方

一般に，高校入試問題では「円周角の定理」を覚えているだけでは，問題は解けません．この問題では，次の2つの定理を組み合わせて解いています． (1) 二等辺三角形の2つの底角は等しい． (2) 円周角は中心角の半分になる． 特に， (1)を使って元の角 x の代わりに，他の角 ∠ BAC で計算する方法が使えるようにしましょう． 右の図において，点 A, B, C は円周上の点① 接線が半径と交わる角度は、90° ② 単曲線の内角は、交角iと等しい ④ 曲線始点bcから、次のno杭以降の各中心杭までの弧長は、中心杭間距離を逐次加えて求め、 交角 I ＝ 1°とし、交点 IPと円曲線の中点との距離を 0mとなるようにしたとき、建問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答

円の周りの長さを計算しよう 家庭学習レシピ

円 角度 求め方

円 角度 求め方-弧長（円弧の長さ）L、弦長d、矢高（円弧の高さ）h、半径rのどれか2つに値を入力して、残りの2つを0と入力すると（空白にはしないでください）、その残りの2つおよび中心角を計算します。 L=r*θ, d=2*r*sin (θ/2), h=r* (1cos (θ/2))を用い、ニュートン・ラフソン法で計算しています。 ※180°以上の中心角の場合、および2つ解がある場合にも対応しました。 動かないA = 面積 L ＝ 弧の長さ α ＝ 角度 (DEG) α ＝ 角度 (rad) 円 A = 面積 D ＝ 外径 d ＝ 内径 楕円 A = 面積 P ＝ 円周 (近似式) 円錐 V = 体積 A = 円錐面積 r ＝ d/2 = 半径 三角錐

円の周りの長さを計算しよう 家庭学習レシピ

Hatena0 高校で習う 三角関数 ですが、当然数学検定でも前提知識として求められます。 三角関数の基本となる、 sin 、 cos 、 tan に関しては 求め方 と 意味 をまずは理解しましょう。 そうする事で後々出てくる公式の直線の傾きと正接(tanθ) 直線の傾きと正接(タンジェント)の関係についてみていきます。 図のような直線、"y=ax"があります。このとき"y=ax"の傾き"a"は、 で求めること つまり、 軸上で円と重なる点を求めましょう。 ↓の図で言うと点cと点dです。 では実際に、点cと点dの値を求めましょう。 円の中心の座標が(50,0)、円の半径が150なので、三平方の定理

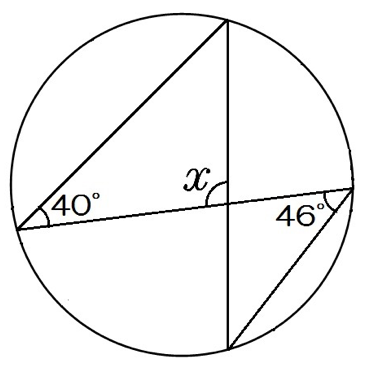
 この円の直径は D=687 cm これより、全円周長さは D･314 =687･314 =2160 その内、円周長さ1 cm分は、全円周長さを 2160/1 =18 等分したもの。 したがって、弧の長さが1 cm、半径3435 cmの扇形の中心角は 360/18 = deg これでよろしいかと思います。100円から読める！ネット不要！印刷しても読みやすいpdf記事はこちら⇒ いつでもどこでも読める！広告無し！建築学生が学ぶ構造力学のpdf版の学習記事 三角関数の角度は？求め方 三角関数の角度は「三角関数の逆関数」で算定できます。直径の円周角は、つねに90° 40°という角度がヒントになっているけれど、同じ弧に対する円周角や中心角も見当たらないし、使いづらく感じてしまうね。 そこで、 ∠xの方を動かす ことを考えよう。 これは、 同じ弧に対する円周角 が存在するよ。 答えが見えてきたかな？ 直径の円周角は、つねに90° 。 つまり、∠x＋40°＝90° だよ。 (2)の答え

解説 例題 6 右図のように同じ大きさの円がそれぞれの円の中心を通るように重なっています。 このときアの角度を求めなさい。 点P , Qは円の中心です。 解説 例題 7 右図のように正方形があり、その中に正方形の一辺を半径とするおうぎ形が2つあり 三角関数の角度の求め方や変換公式！ 計算問題も徹底解説 21年2月19日 この記事では、三角関数について、角度の求め方や変換公式（ など）について解説していきます。 計算問題もわかりやすく説明していくので、この記事を通してぜひマスターして 円錐の体積の求め方がわかる3つのステップ つぎの例題をときながらみていこう！ Step1 円錐の「底面積」を計算するっ！ まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、 円の面積の公式 をつかって

中学３年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生

円の周りの長さを計算しよう 家庭学習レシピ

 正弦 (sin)余弦 (cos)正接 (tan)の求め方 B!この問題を見て，逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め， 両者を比較しようと考えた方が多いのではないでしょうか． しかしこの問題では，角度そのものではなく角度差の符号を求めればよいので， 逆三角関数を使う方法よりも簡単で優れた，外積 cはいきなり求めることができないので、dの角度を求めてから考えます。dはbと同位角の関係になるので、 d＝60° 直線の角の大きさは180°です。そのためcの角度は、180°60°＝1° よって、 答え a＝60°、b＝60°、c＝1° 例題3 下の四角形のaの角度を求めなさい。

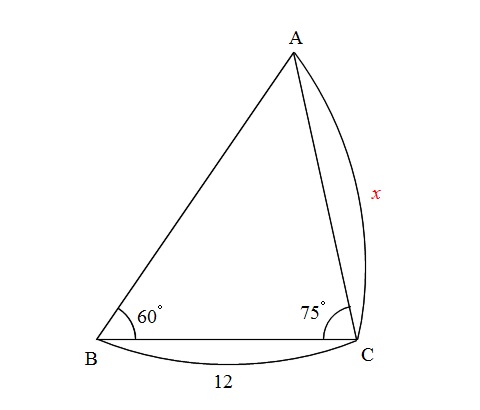
三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない

円に内接する四角形の性質まとめ 対角の和が180 になる理由 アタリマエ

一般に使われているコピー用紙 （1）上記の図のようにまず紙の中央に折り目を付けてください。 （2）紙の長辺の2つの角が弧の曲線に触れるように配置ください（テープ等で留めてください）。 ※下の写真の 〇 部分 （3）紙の折り目のついた中央部分円の面積 ＝ 半径 × 半径 × 円周率 弧の面積 まず、円の面積を求めて、そのうちの弧の角度分の 三角旗とブーメランを見つければ、基本問題はバッチリ!!今回は図形の角度を求め方の説明です。 今回ポイントとなるのは「三角形の内角と外角」の関係です。 丁寧な説明を心がけた結果，解説中の図がとても多くなってしまいましたが，ゆっくり読んでいただければVideos you watch may be added to the TV's watch history and influence TV recommendations To avoid this, cancel and sign in to on your computer Cancel Confirm Switch camera Share

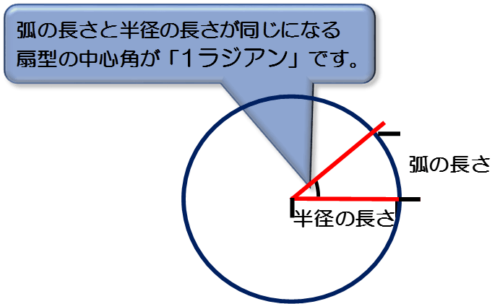
ラジアン 弧度法 の意味と 度 への変換方法

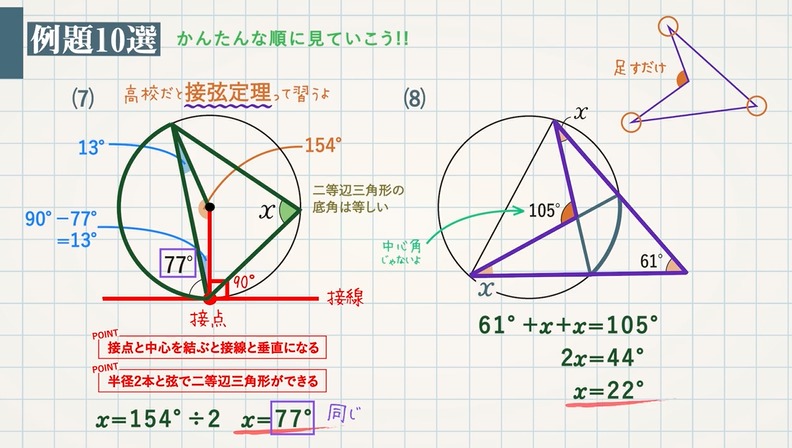
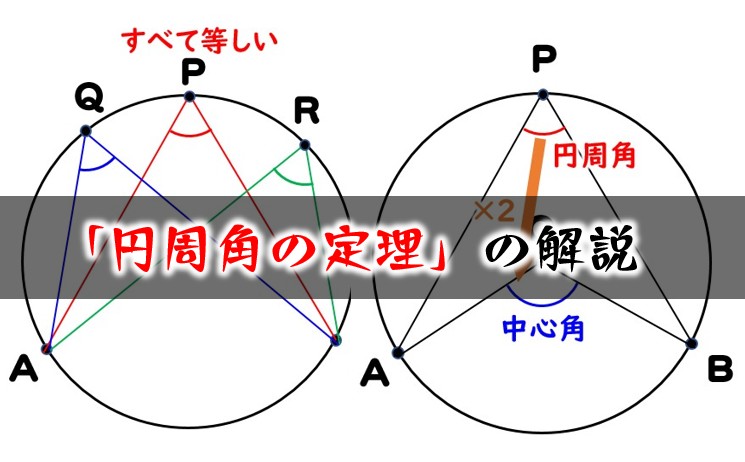
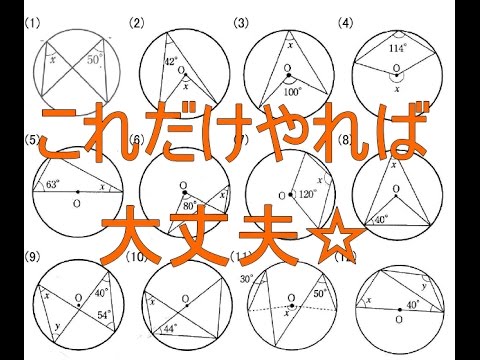
円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

概要 三角関数（度） サイン、コサイン、タンジェントなどの三角関数を度単位で計算します。 三角関数（グラフ） sin、cos、tanの関数表を計算し、sinとcosのグラフを表示します。 逆三角関数（度） アークサイン、アークコサイン、アークタンジェントなどの逆三角関数を度単位で計算します。 角度と底辺から斜辺と高さを計算 直角三角形の底辺と傾斜角から中心角92°が書いてあって，円周角が書いてないときは，92°÷2= 46° で円周角が求まります． 円周角46°が書いてあって，中心角が書いてないときは，46°×2= 92° で中心角が求まります．円柱の体積、表面積の求め方はこれでバッチリ！ 円錐の表面積、中心角の求め方を解説！裏ワザ公式も！←今回の記事 円錐を転がすと1周するのにどれくらい回転する？ 球の体積・表面積の公式はこれでバッチリ！語呂合わせで覚えちゃおう！

円周角の定理の証明 3つのパターンから分かる円周角と中心角の関係性 アタリマエ

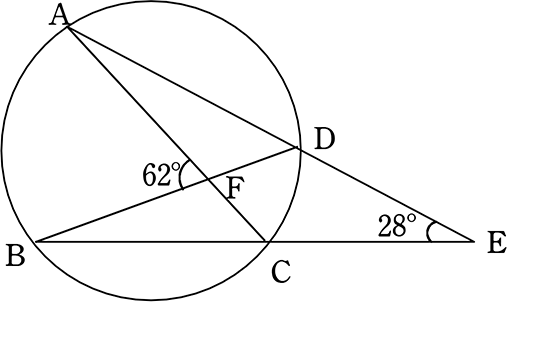
中学数学 円周角 中心角

 円の円周と扇の弧の長さは等しい 円錐の中心角の求め方は、 扇部分の半径・弧の長さを求める (扇の中心角を求める問題になる) 中心角を求める はかせちゃん 今日もお疲れ様でした！ 抹茶ラテ飲んでゆっくりしましょ～ 関連記事はこちら 中学数学下図のように、中心oを通る直線と円との交点をdとします。 円に内接する四角形の対角の和は180°なので ・・・① となります。また1で証明した接弦定理を使うと ・・・② となり、直進の角度は180°なので ・・・③ となります。①、②、③を足せば②正多角形のかき方 ③円周率の求め方(円の円周と直径の関係） ④円周や直径の求め方 ⑤生活の中で円周を求めるよさ 教え方1 正六角形や正八角形を作らせながら、正六角形や正八角形の意味をとらえさせます。 動画を見せて六角形のつくり方を説明し、

円周角の定理 証明 逆をスマホで見やすい図で徹底解説 高校生向け受験応援メディア 受験のミカタ

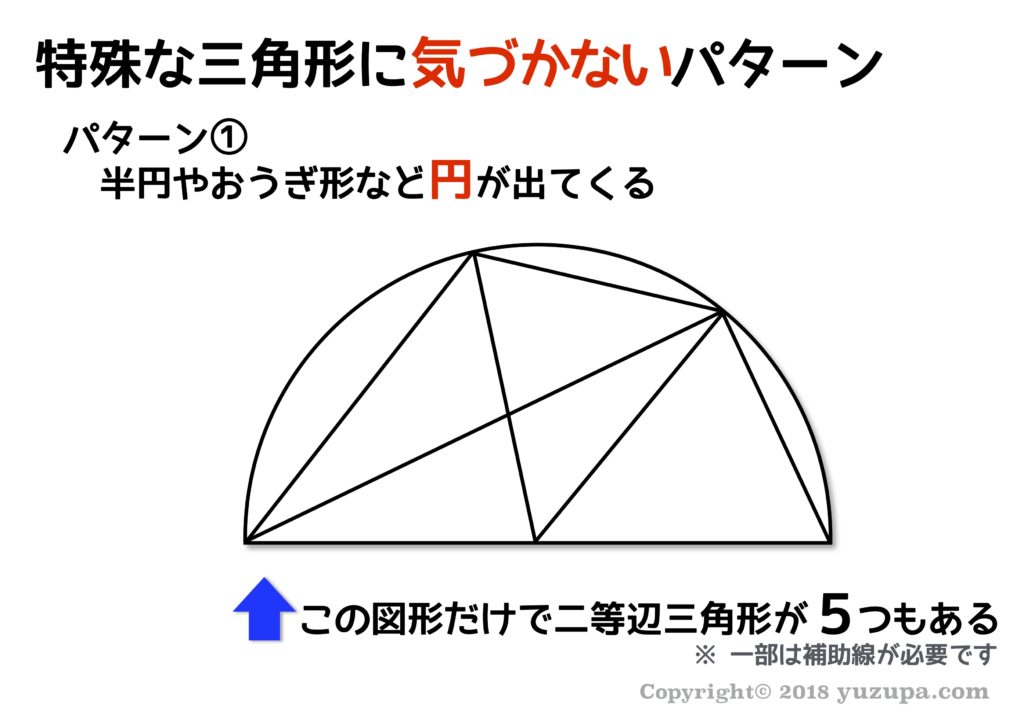
中学受験 図形の角度問題は ７つ道具 で攻略 かるび勉強部屋

 角度別に分かるその証明方法 18年8月9日 「円の接線 A T と弦 A B が作る角 ∠ B A T は、弦 A B に対する円周角 ∠ A C B と等しい」という定理を、 接弦定理 と言います。続いて扇の面積について考えてみましょう。 円の面積はr×r×πで求められました。 先ほどと同じように考えます。 2πの角度のときにその面積はr×r×πです。 では角度がθのときはどうなるでしょうか。 2π：r×r×π＝θ：S これを整理すると ②（ただし

円周角の定理の解説 問題の解き方 数学fun

外接円の半径の求め方がイラストで誰でも即わかる 練習問題付き 高校生向け受験応援メディア 受験のミカタ

円周率pが現われる世界 ３ Pが角度180 ってどういう意味 研究員の眼 ハフポスト

10年06月の記事 日曜土木検史郎参上

6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4

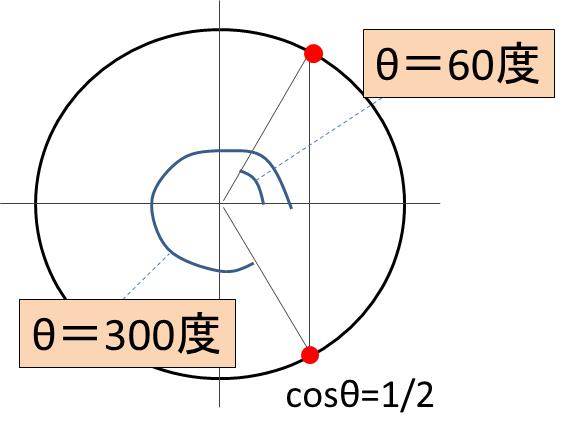
Cos8 1 2の角度 8の値 は Cos8 ルート3 2やcos8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム

円周角の定理 円に内接する図形の角度を求める問題を攻略しよう みみずく戦略室

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

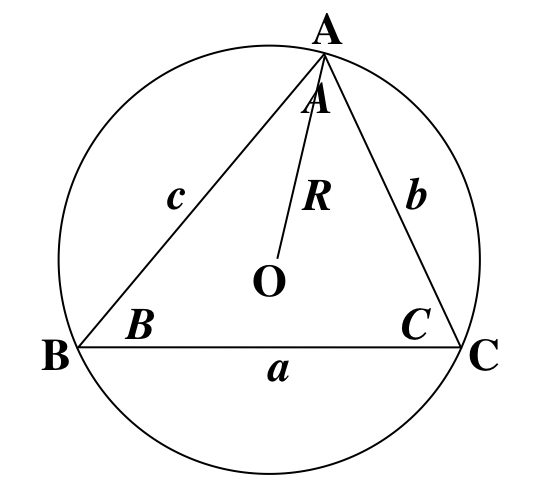
三角比 正弦定理と余弦定理を詳しく解説 スタディクラブ情報局

円の中にある二つある三角形の角度の求め方 Okwave

角の大きさ 小学４年 手間がかかりますが 丁寧に 算数の教え方教えますmother S Math Happy Study Support

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名

中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット

円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に

余弦定理で角度を求める方法 数学の星

1

1

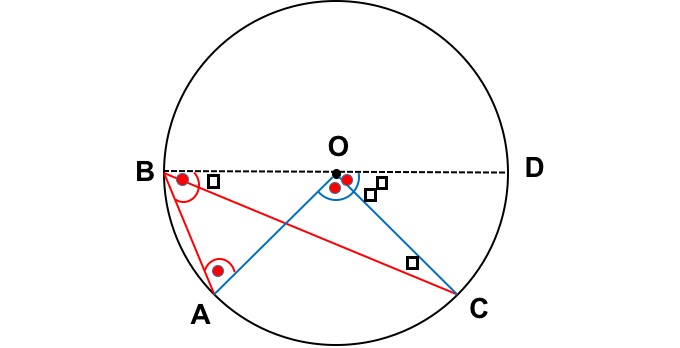
円周角の定理と証明 中心角の求め方を詳しく解説 Rikeinvest

1

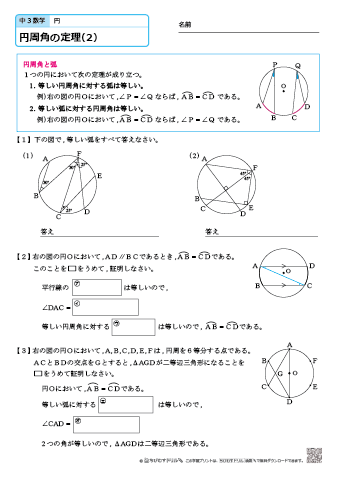
中学３年生 数学 円周角の定理 練習問題プリント ちびむすドリル 中学生

円周角の定理 円の中にブーメラン型があるときの角度の求め方 数スタ

垂心について

中3数学 円周角の定理の逆 の重要ポイント 映像授業のtry It トライイット

円の弧長 弦長 矢高 半径のどれか2つを与えて残りを計算 高精度計算サイト

Xの角度の求め方を教えてください 3 と 5 です 円周角の問題です Clear

6本の缶を最短の紐で束ねる意外な方法とは 円と球の不思議な雑学 横山 明日希 ブルーバックス 講談社 1 4

三角関数の角度は 3分でわかる求め方 公式と計算 表との関係

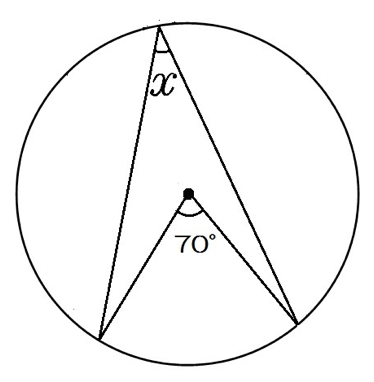
円の性質 円周角の角度の求め方の3つのパターン Qikeru 学びを楽しくわかりやすく

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

扇形の弧の長さの求め方 公式と計算例

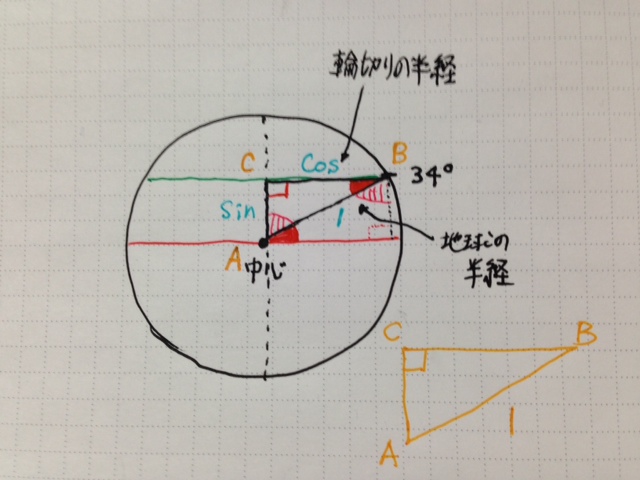
経度１度あたりの距離の計算 電気ウナギ的

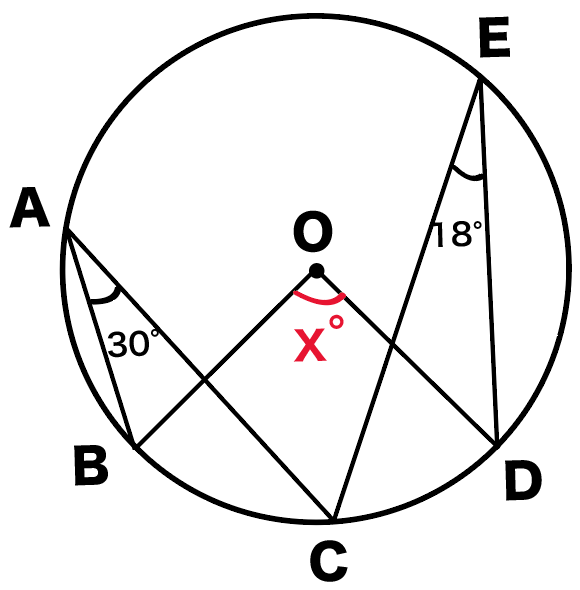
円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ

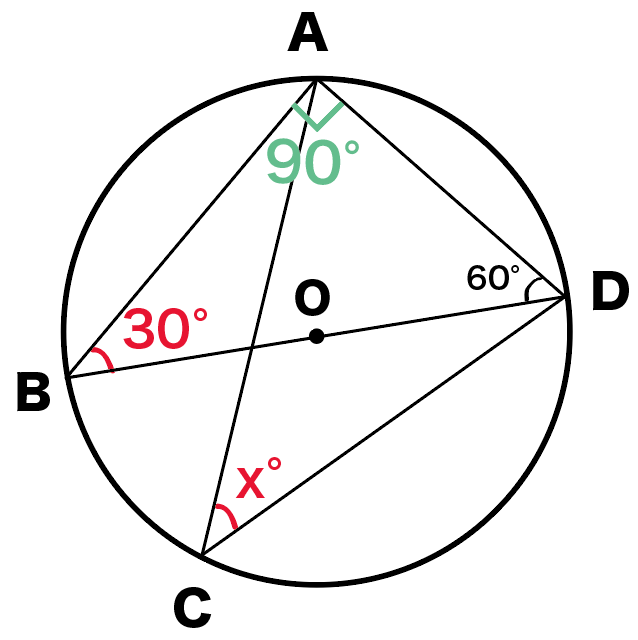
円周角の定理で角度を求める問題の解き方3ステップ Qikeru 学びを楽しくわかりやすく

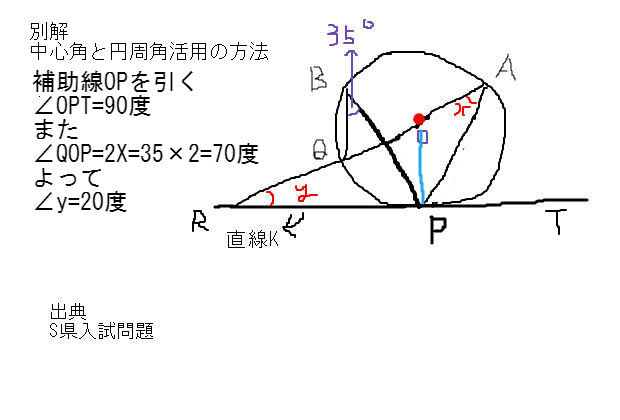
接弦定理活用 正答率14 問題をあっさり速答方法 制限１分 中学数学 理科 寺子屋塾の復習サイト

円周角の定理 角度の計算 中学数学 Youtube

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

外接円 外心について

七五三 三角形から円に内接する四角形へ

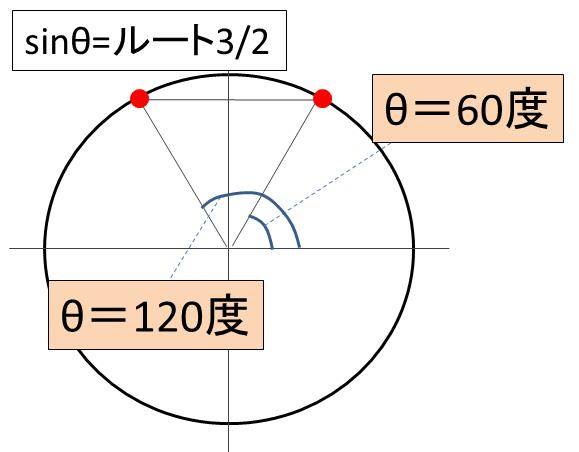
Sin8 1 2の角度 8の値 は Sin8 ルート3 2やsin8 1 ルート2 ルート2分の1 を満たす角度は何度 単位円 ウルトラフリーダム

Xの角度の求め方を教えてください 円周角の定理を使う問題です Clear

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

弓形の面積 香料ゐっすゐの夢

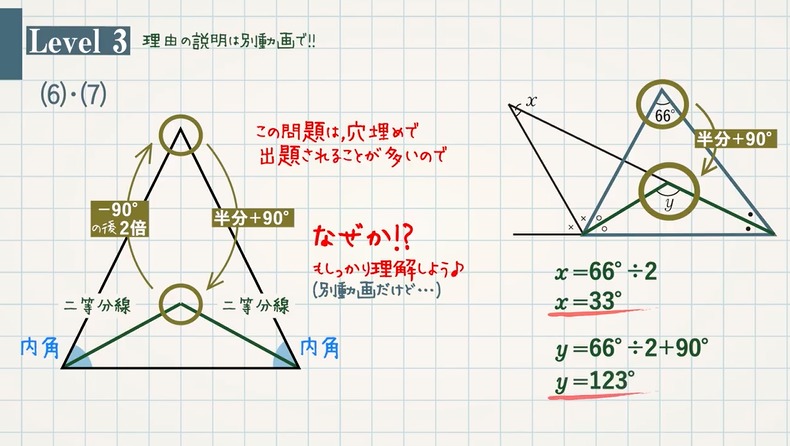
角度の計算 裏技まとめ 教遊者

内心とは 三角形の内心の求め方や比の使い方 性質の証明 位置ベクトルをわかりやすく解説 遊ぶ数学

円の中に三角形角度の求め方 いろんな角度の三角関數を単位円で考える Qmog Fi

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

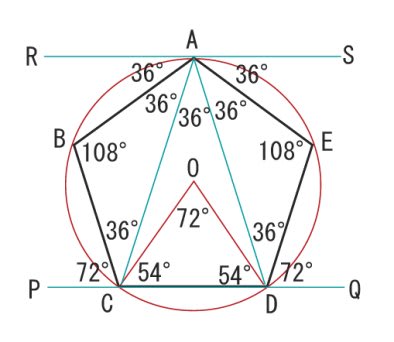
正五角形というだけで 分かる角度は 名寄 算数数学教室より

円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

扇形の中心角の求め方がわからない 比例を理解できれば公式無しでも大丈夫 中学受験ナビ

平面図形 おうぎ形の中心角の求め方 中学数学 定期テスト対策サイト

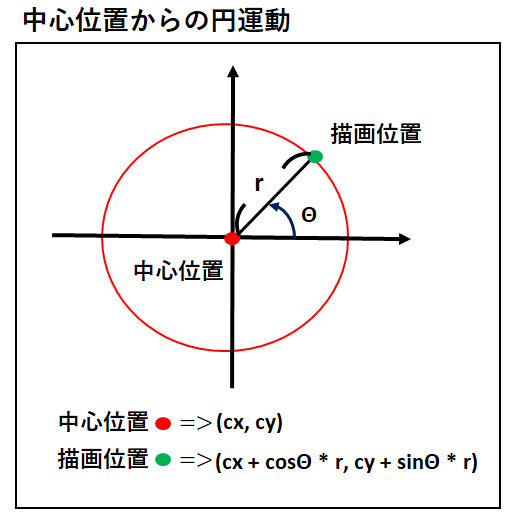
ゲーム 円運動

おうぎ形の弧の長さ 面積 中心角の求め方と公式 Irohabook

数学 円すいの展開図 扇形の中心角は5秒で出せる 受験の秒殺テク 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

8の角度求め方教えてください 答えは70 です Clear

円周の公式 なぜ直径 円周率で計算できるのか 円周率を調べる方法 数学fun

円周角の定理 円周角と中心角の関係は中学や高校でよく出るぞ 中学や高校の数学の計算問題

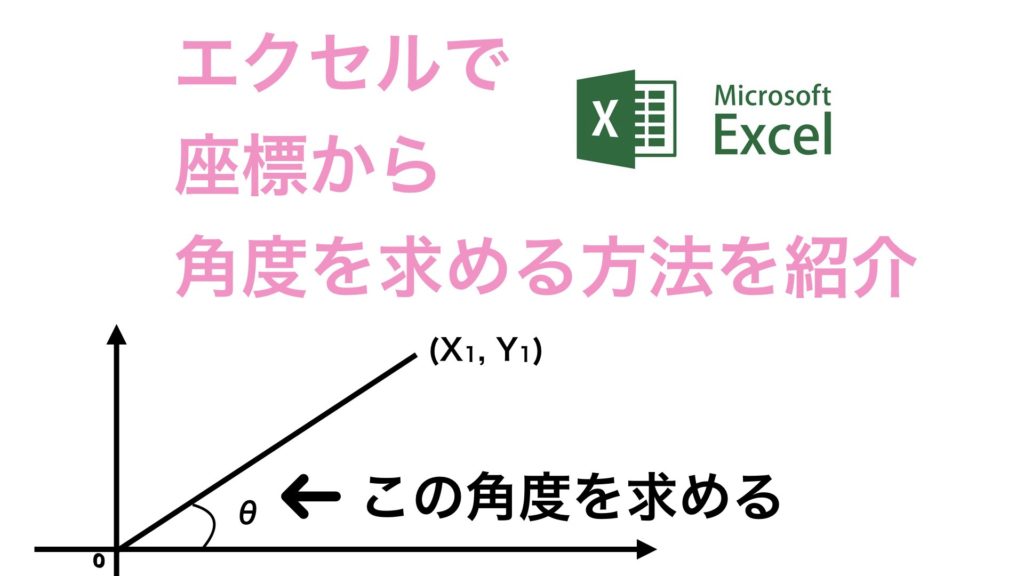
エクセルで座標から角度を求める方法 しおビル

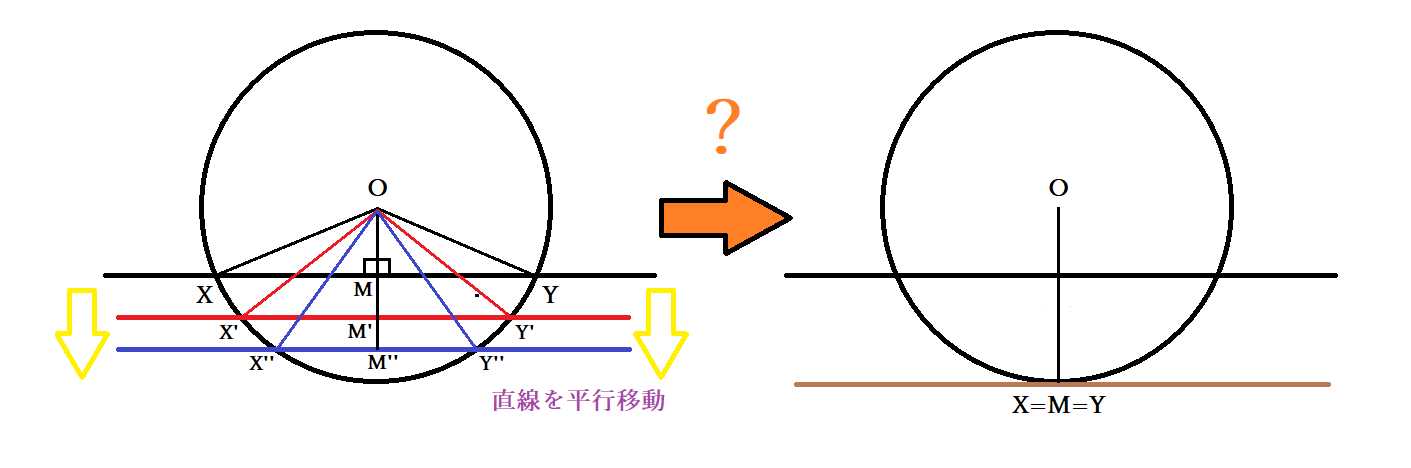
数学 円の接線の角度が90度 直角 であることの証明 接線とは 円と直線の接点とは Curlpingの幸せblog

円周角の定理と中心角 中学３年数学 Youtube

三角形 の 角度 を 求める ニスヌーピー 壁紙

中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット

三角形 角度 の 求め 方 三角関数 機械加工でよく使う計算方法を説明します Documents Openideo Com

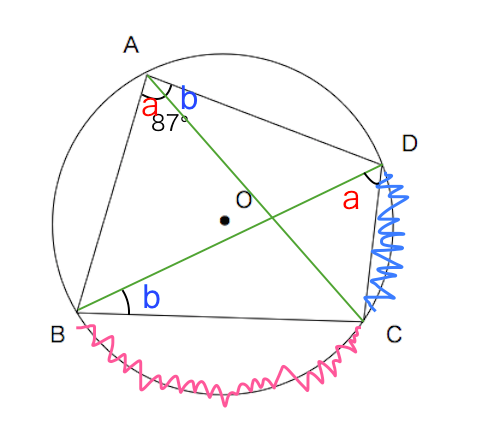
円に内接する四角形 苦手な数学を簡単に

1

ラングレーの問題 整角四角形

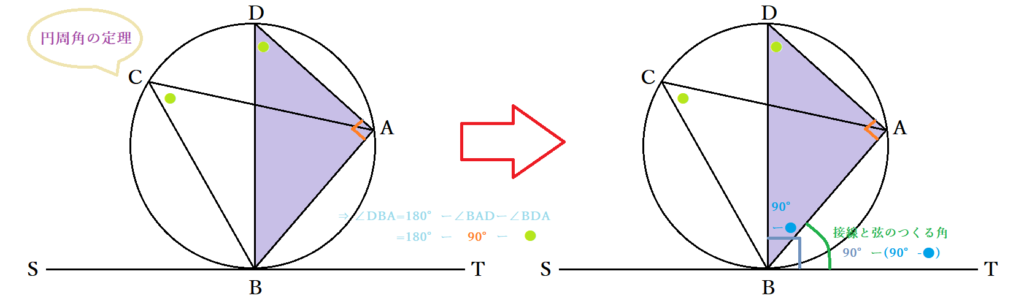
接弦定理とは 接線と弦の作る角の定理の証明 覚え方と応用問題 中学 高校 Curlpingの幸せblog

三角関数とは 1分でわかる意味 公式と計算 角度と値の関係

Xの求め方と答えを教えてください Clear

数学ａの円で使う定理 性質の一覧 数学a By となりがトトロ マナペディア

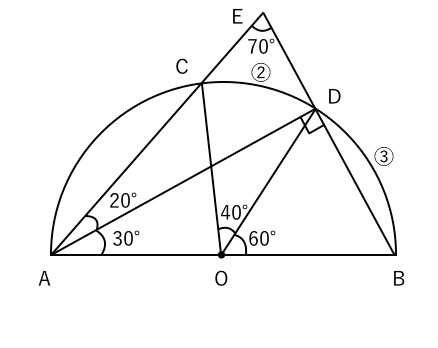
円周角と比の問題 苦手な数学を簡単に

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

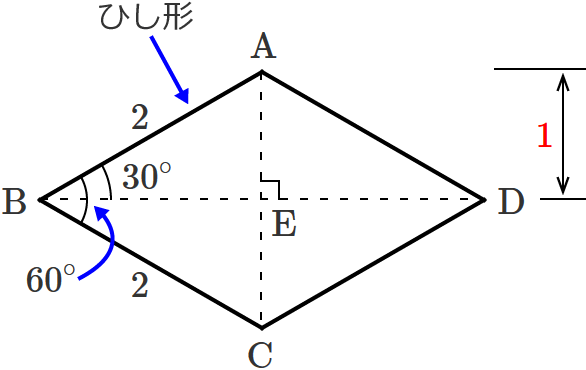
ひし形の対角線の長さの求め方

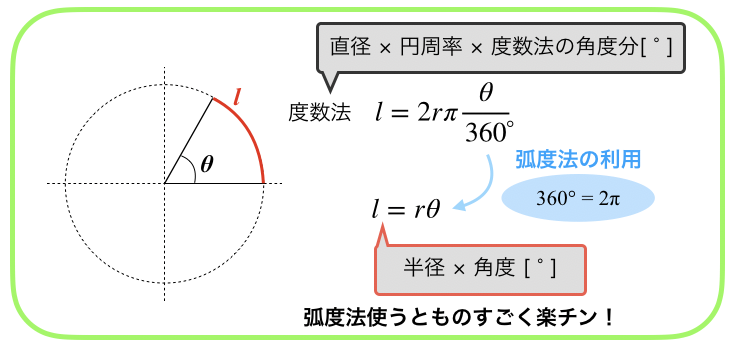
弧度法ってなんだよ ラジアンってなんだよ ってなっている君へ 動画解説あり

小学4年生 角度の求め方は 対頂角 平行線 同位角 錯角 中学受験 そうちゃ式 受験算数 2号館 図形 速さ

Xの角度の求め方を教えて下さい Clear

円周角の定理とは 円周角の定理の証明や問題の解き方を完全解説 Studyplus スタディプラス

三角関数で角度から座標を導くふたつの式の使い途 Qiita

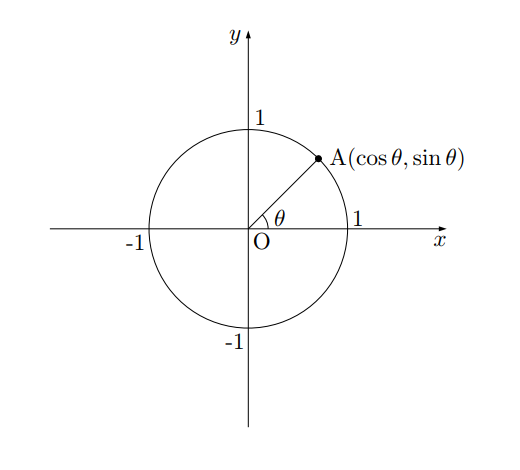
Tanとは Tanを単位円で考えるとどうなるか 高校数学の知識庫

開発メモ 円周上の点 自由処

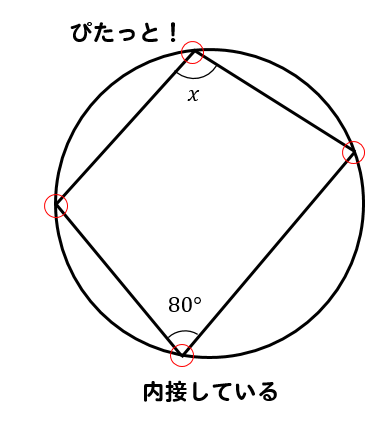
これで10点アップ 円周角の定理とは 問題の解き方はどうやるのかパターン別に解説 数スタ

斜辺10cm 高さ6cmの ありえない 直角三角形の面積を真面目に求める

円 半円 弧 扇形 の円周 面積の求め方と公式一覧 小学生の算数 Yattoke 小 中学生の学習サイト

この問題のxの角度の求め方を教えてください 答えは62度です Clear

接弦定理とは何か 角度別に分かるその証明方法 アタリマエ

中3数学 円の角度の求め方 練習編 映像授業のtry It トライイット

円周の求め方 公式と計算例

円周角の定理と角度を求める問題10選 中心角 ターレスの定理 内接する四角形 教遊者

エクセルで用いる角度の単位は 度 ではない 売上予測の基礎の基礎 3 売上予測 ３０年の実績

Incoming Term: 円 角度 求め方, 円 接線 角度 求め方,